滤镜Shader——像素卷积变换

发表于 | 分类于 |

像素卷积变换，常见的滤镜效果包括边缘检测、高斯模糊、锐化等。从我的理解上卷积就是一种数学运算，它运用在图像处理中可以让不同的图像滤波器通过卷积运算而获得相应的滤波效果。

接下来详细学习一下卷积的概念以及如何通过它实现几个滤镜效果，这里代码部分就使用之前编写的Metal滤镜处理框架。

卷积运算

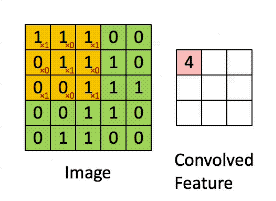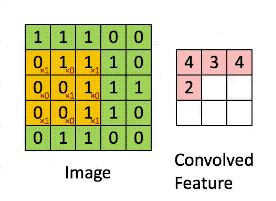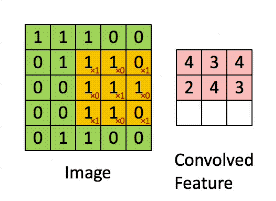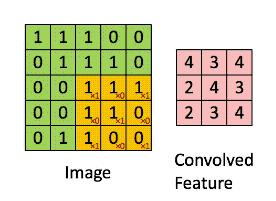
数字图像是一个二维的离散信号，对数字图像做卷积操作其实就是利用卷积核（卷积模板）在图像上滑动，将图像点上的像素灰度值与对应的卷积核上的数值相乘，然后将所有相乘后的值相加作为卷积核中间像素对应的图像上像素的灰度值，并最终滑动完所有图像的过程。

还有一种说法，图像卷积就是一个加权平均的过程。

正如下图我们使用下面这个卷积模板进行图像卷积运算，其结果就如动图那样，每个像素值都进行了加权平均运算。
$$
\left[
\begin{matrix}
1 & 0 & 1 \\
0 & 1 & 0 \\
1 & 0 & 1
\end{matrix}
\right]
$$

-l

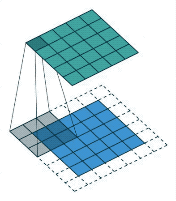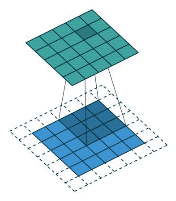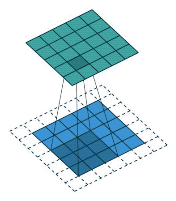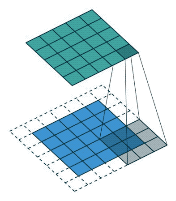
几种不同卷积核实现的效果

下面几种效果的本质区别只在于它们进行卷积运算的卷积模板（或者说它们在频域处理用的滤波器）不同。

边缘检测

边缘检测是图像处理和计算机视觉中的基本问题，边缘检测的目的是标识数字图像中亮度变化明显的点。图像属性中的显著变化通常反映了属性的重要事件和变化。这些包括深度上的不连续、表面方向不连续、物质属性变化和场景照明变化。

图像边缘检测大幅度地减少了数据量，并且剔除了可以认为不相关的信息，保留了图像重要的结构属性。有许多方法用于边缘检测，它们的绝大部分可以划分为两类：基于查找一类和基于零穿越的一类。

显然我们认为一个像素点是否为边缘点的依据就是看这个像素在周围是否是变化明显的点，也就是在这个位置上它的变化率是否是突变的。

这里我们使用Prewitt算子的做一个简单的边缘检测，其中Prewitt算子是一种一阶微分算子，它的基本原理就是利用差分的定义f'(x) = f(x + 1) - f(x)。

将它转化一阶矩阵表示就是[-1 f(x-1)，0 f(x)，1 * f(x+1)]，提取出系数[-1, 0, 1]再转为二阶矩阵即可表示为矩阵形式:
$$
\left[
\begin{matrix}
-1 & 0 & 1 \\
-1 & 0 & 1 \\
-1 & 0 & 1
\end{matrix}
\right]\tag{水平方向}
$$

$$
\left[
\begin{matrix}
1 & 1 & 1 \\
0 & 0 & 0 \\
-1 & -1 & -1
\end{matrix}
\right]\tag{垂直方向}
$$

高斯模糊

高斯模糊效果是让图像与正太分布做卷积运算使得图像呈现出模糊的效果。通过利用正太分布曲线以待处理的像素点为中心原点对它四周像素按照权重进行重新采样。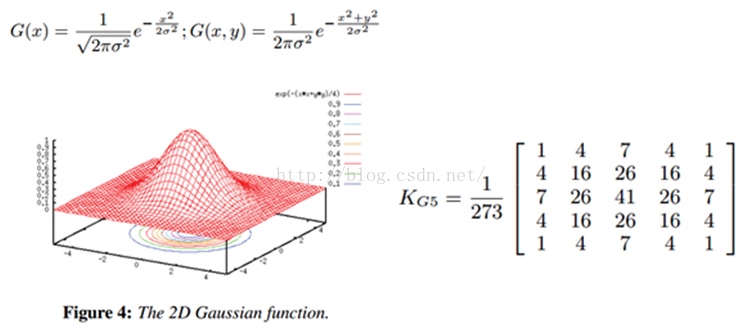

锐化

锐化效果是让图像的边缘上的像素比周围的像素有更高的对比度，使用下面的边缘锐化卷积模板生成的边缘锐化效果。
$$
\left[
\begin{matrix}
0 & -1 & 0 \\
-1 & 5*n & -1 \\
0 & -1 & 0
\end{matrix}
\right]
$$

一个通用的卷积处理模板

这里我们参考Metal Performance Shaders框架中的MPSImageConvolution实现一个简单的卷积运算滤镜。

根据MPSImageConvolution中的描述，它的卷积模板规定为奇数的宽度和高度，对于3x3, 5x5, 7x7, 9x9, 11x11, 1xN和Nx1这种常见的卷积模板进行了算法复杂度优化而其他情况则是MxN的算法复杂度，同时一个卷积模板还可以分解为两个向量进行叠加运算。

那么具体要如何实现呢？对图像处理而言，存在两大类的方法:空域处理和频域处理。空域处理是指直接对原始的像素空间进行矩阵计算，频率处理是指先对图像变换到频域，再做滤波等处理。

接下来我们尝试动态生成Metal脚本在空域进行矩阵计算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
+ (NSString *)vertexShaderWithKernelWidth:(NSUInteger)kernelWidth
                             kernelHeight:(NSUInteger)kernelHeight {
    
    // 顶点着色器返回参数结构体
    NSMutableString *shaderString = [[NSMutableString alloc] init];
    [shaderString appendFormat:@"using namespace metal;\n"];
    [shaderString appendFormat:@"struct ConvolitionVertexIO {\n"];
    [shaderString appendFormat:@"   float4 position [[position]];\n"];
    [shaderString appendFormat:@"   float2 textureCoordinate [[user(texturecoord)]];\n"];
    for (int i = 0; i < kernelWidth; i++) {
        for (int k = 0; k < kernelHeight; k++) {
            [shaderString appendFormat:@"   float2 coordinates_%d_%d;\n", i, k];
        }
    }
    [shaderString appendFormat:@"};\n"];
    
    // 采样单位步长，一般认为{1.0/width, 1.0/height}
    [shaderString appendFormat:@"struct ConvolitionParameter {\n"];
    [shaderString appendFormat:@"   float texelWidthOffset;\n"];
    [shaderString appendFormat:@"   float texelHeightOffset;\n};\n\n"];
    
    // 顶点着色器脚本
    [shaderString appendFormat:@"vertex ConvolitionVertexIO convolitionVertex(device packed_float2 *position [[buffer(0)]],\n"];
    [shaderString appendFormat:@"                                             device packed_float2 *texturecoord [[buffer(1)]],\n"];
    [shaderString appendFormat:@"                                             constant ConvolitionParameter &para [[buffer(2)]],\n"];
    [shaderString appendFormat:@"                                             uint vid [[vertex_id]]) {\n"];
    [shaderString appendFormat:@"   ConvolitionVertexIO outputVertices;\n"];
    [shaderString appendFormat:@"   outputVertices.position = float4(position[vid], 0, 1.0);\n"];
    [shaderString appendFormat:@"   outputVertices.textureCoordinate = texturecoord[vid];\n"];
    
    // 生成卷积矩阵对应的坐标
    int offset = 0;
    CGPoint kernelIndex = CGPointMake(floor(kernelWidth / 2.0), floor(kernelHeight / 2.0));
    for (int i = 0; i < kernelHeight; i++) {
        for (int k = 0; k < kernelWidth; k++, offset++) {
            int distanceX = k - (int)kernelIndex.x, distanceY = i - (int)kernelIndex.y;
            [shaderString appendFormat:@"   outputVertices.coordinates_%d_%d = texturecoord[vid] + float2(para.texelWidthOffset * %d, para.texelHeightOffset * %d);\n", k, i, distanceX, distanceY];
        }
    }
    [shaderString appendFormat:@"   return outputVertices;\n}\n"];
    
    return shaderString;
}

+ (NSString *)fragmentShaderWithKernelWidth:(NSUInteger)kernelWidth
                               kernelHeight:(NSUInteger)kernelHeight
                                    weights:(const float *)kernelWeights {
    // 片段着色器脚本
    NSMutableString *shaderString = [[NSMutableString alloc] init];
    [shaderString appendFormat:@"fragment half4 convolitionFragment(ConvolitionVertexIO fragmentInput [[stage_in]],\n"];
    [shaderString appendFormat:@"                                   texture2d<half> inputTexture [[texture(0)]]) {\n"];
    [shaderString appendFormat:@"   constexpr sampler quadSampler;\n"];
    [shaderString appendFormat:@"   half4 sum = half4(0.0);\n"];
    
    int offset = 0;
    for (int i = 0; i < kernelHeight; i++) {
        for (int k = 0; k < kernelWidth; k++, offset++) {
            float weight = kernelWeights[offset];
            [shaderString appendFormat:@"   sum += inputTexture.sample(quadSampler, fragmentInput.coordinates_%d_%d) * %f;\n", k, i, weight];
        }
    }
    [shaderString appendFormat:@"   return sum;\n}\n"];
    
    return shaderString;
}

参考

【信号与系统】卷积积分这样学！
通俗理解『卷积』——从傅里叶变换到滤波器
图像卷积与滤波的一些知识点
理解图像卷积操作的意义
DL 入门：再次理解「卷积」过程
图像处理的几个基本概念——卷积、滤波、平滑

如何识别图像中的边缘
边缘检测原理 - Sobel, Laplace, Canny算子
数字图像图像处理:边缘检测(Edge detection)
几种边缘检测效果